Source: Complete International Mathematics For Cambridge IGCSE - David Rayner, Jim Fenson

CALCULATING ANGLESPARALLEL LINES PYTHAGORAS THEOREM 
SIMILARITY AND CONGRUENCYarEAS of similar shapesVOLUMES of similar shapes
 past paper questions 

BASIC CONCEPTS:

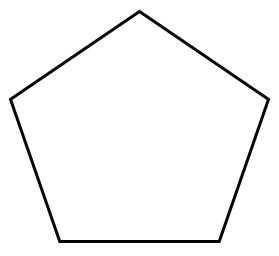n = 5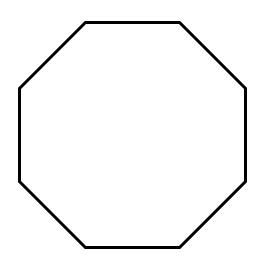       
 
                  n = 8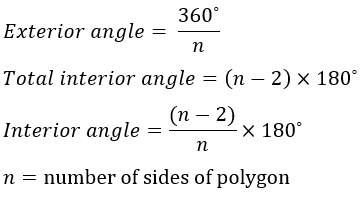
 


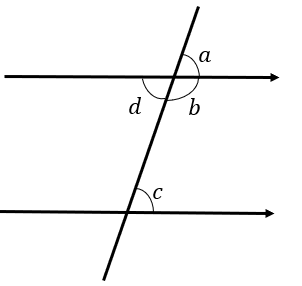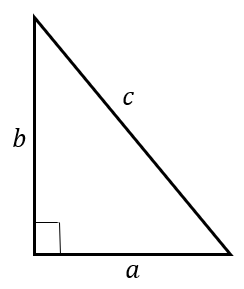ROTATIONAL SYMMETRY: THE PROPERTY BY WHICH AN OBJECT WHEN TURNED THROUGH AN ANGLE (LESS THAN ONE FULL TURN) AND STILL LOOKS THE SAME IS CALLED ROTATIONAL SYMMETRY


ORDER OF ROTATIONAL SYMMETRY: THE NUMBER OF TIMES IT CAN BE ROTATED AROUND A CIRCLE AND STILL LOOK THE SAME.


  SHAPESIDES  ANGLES SYMMETRY
 ROTATIONAL 
SYMMETRY
DIAGONALS 
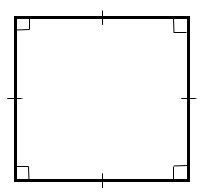 SQUAREALL SIDES ARE
EQUAL
OPPOSITE SIDES
ARE PARALLEL		ALL ANGLES
ARE EQUAL.
ALL ANGLES = 90°		FOUR LINES OF 
SYMMETRY		ORDER 4 DIAGONALS BISECT
 AT RIGHT ANGLES
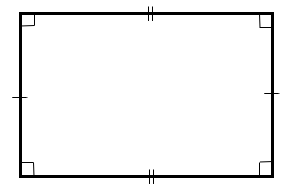 RECTANGLEOPPOSITE SIDES 
ARE EQUAL AND 
PARALLEL 		ALL ANGLES 
ARE EQUAL.
ALL ANGLES = 90° 		TWO LINES OF 
SYMMETRY 		 ORDER 2DIAGONALS BISECT
EACH OTHER 
 
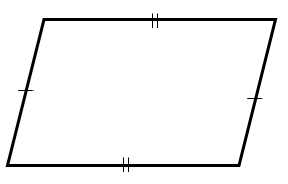 PARALLELOGRAMOPPOSITE SIDES 
ARE EQUAL AND
PARALLEL		OPPOSITE ANGLES 
ARE EQUAL 		NO LINES OF 
SYMMETRY		ORDER 2  DIAGONALS BISECT
 EACH OTHER
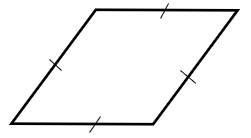 RHOMBUSALL SIDES ARE
EQUAL 
OPPOSITE SIDES
PARALLEL
OPPOSITE ANGLES 
ARE EQUAL  		TWO LINES OF 
SYMMETRY  		 ORDER 2DIAGONALS BISECT
EACH OTHER 
AT RIGHT ANGLES 
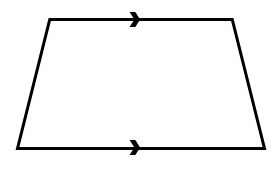 TRAPEZIUM ONE PAIR OF
 SIDES PARALLEL		 -NO LINES OF 
SYMMETRY   		- -
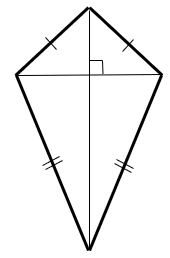KITE TWO PAIRS OF
ADJACENT SIDES
EQUAL 		ONE PAIR OF EQUAL
OPPOSITE ANGLES

ONE LINE OF 
SYMMETRY  		- DIAGONALS MEET AT
RIGHT ANGLES,
BISECTING ONE OF
THEM 

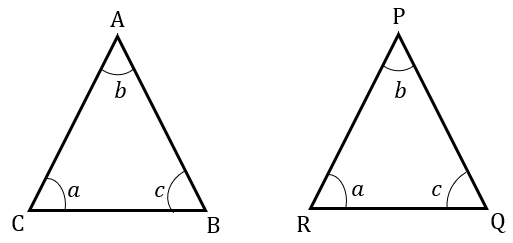
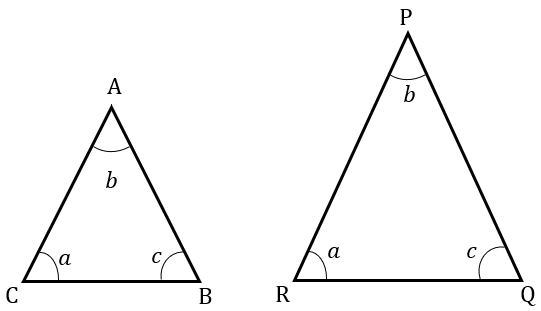TWO TRIANGLES ARE SIMILAR IF THEY HAVE
THE SAME ANGLES. 
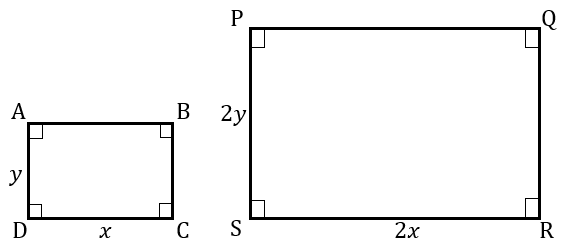TWO RECTANGLES (OR ANY TWO SHAPES) ARE
SIMILAR IF THEY HAVE THE SAME ANGLES AND
CORRESPONDING SIDES ARE IN PROPORTION
TWO POLYGONS ARE CONGRUENT IF ONE FITS
EXACTLY ON THE OTHER. THEY MUST BE THE
SAME SHAPE AND SIZE. 
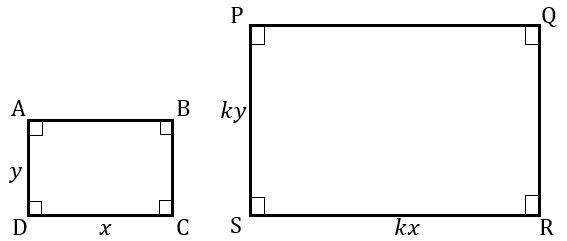 REACTANGLES ABCD & PQRS ARE SIMILAR.
THE RATIO OF CORRESPONDING SIDES IS k.
HENCE THE RATIO OF THEIR AREAS IS k²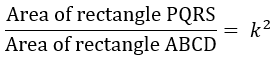

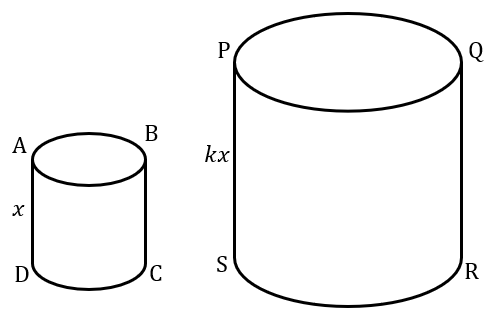 WHEN TWO OBJECTS ARE SIMILAR AND THE
RATIO OF THEIR CORRESPONDING SIDES IS k,
THEN THE RATIO OF THEIR VOLUMES IS k³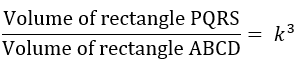


BACK TO TOP