Source: Questions from Complete International Mathematics For Cambridge IGCSE - David Rayner, Jim Fenson
Find the distance and bearing of the finishing point from the starting point.
The Aircraft is at a distance of 953.8 km from the starting point.
The bearing of the finishing point is 180 - 47 = 133°
5. From the top of a tower 75 m, a man sees two goats, both due west of him.
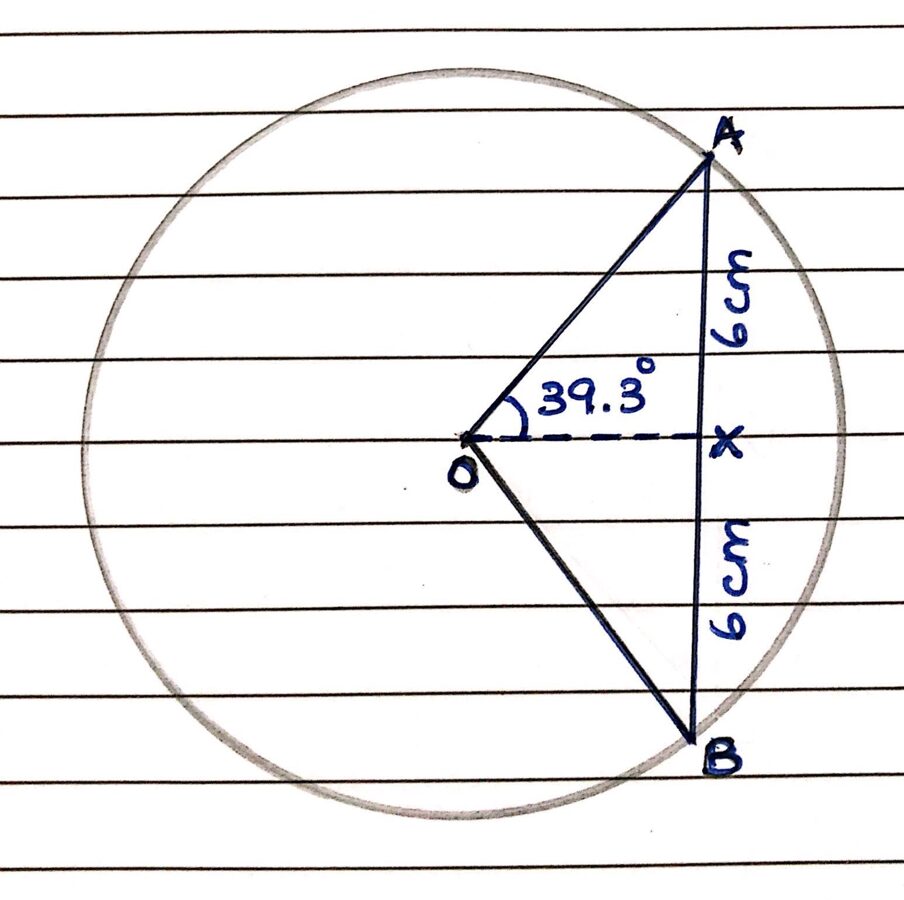
6. A Chord of length 12 cm subtends an angle of 78.6°at the center of the circle.
Find the radius of the circle.
Radius of circle = 9.5 cm
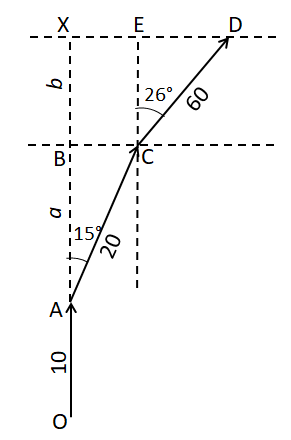
7. A rocket flies 10 km vertically, then 20 km at an angle of 15° to the vertical and finally 60 km at an angle of 26° to the vertical. Calculate the vertical height of the rocket at the end of the third stage.
Vertical height of the rocket at the end of third stage = 83.2 km
9. Diagram A shows a kitchen floor tiled with regular octagons and squares.
Diagram B shows and enlarged view of one octagon.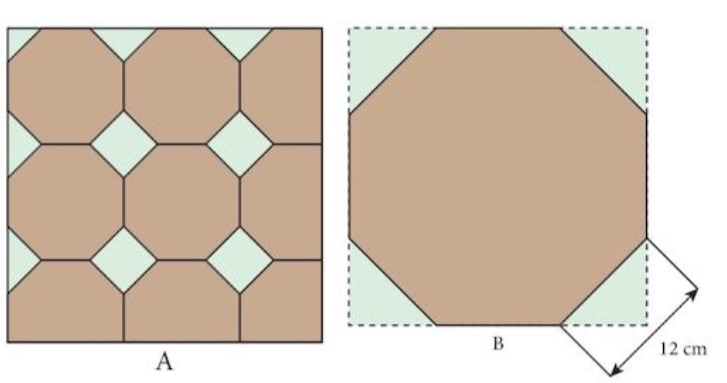
The smaller green squares have sides of length 12 cm.
Find the width of the octagons.
10. A farm gate is 1.3 m high.
y = 113.6 cm
Width of gate = 255 cm
Highest point of stone above ground = 2.7 + 0.45 = 3.13 m
The depth of water when BC is horizontal = 27.12 cm
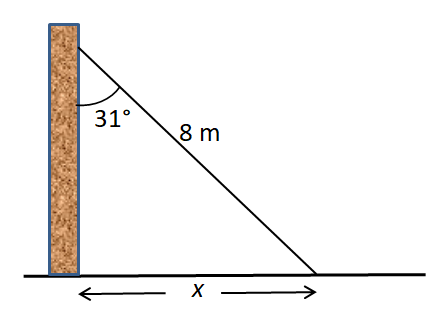
1. A ladder of length 8 m rests against a wall so that the angle
between the ladder and the wall is 31°.
How far is the base of the ladder from the wall?
 | Let the base of ladder be x m from the wall The ladder, the wall and the floor form a triangle 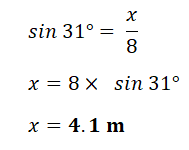 |
The base of the ladder is 4.1 m from the wall.
2. A ship sails 200 km on a bearing of 243.7°.
a) How far south has it traveled?
b) How far west has it traveled?
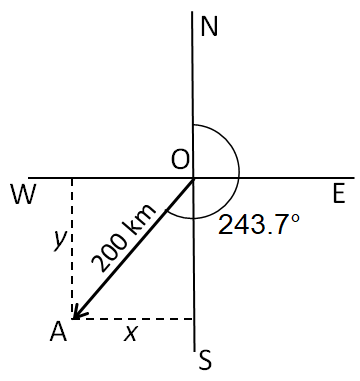 | Let OA be the line traveled by the ship. N, E, S and W represent the North, East, south and West directions respectively Bearing of ship = 243.7°( The line of travel of ship makes an angle of 243.7° measured clockwise from North) North-South is a straight line = 180° 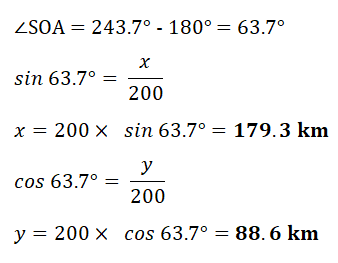 |
The Ship has traveled 88.6 km to the south and 179.3 km to the west.
Find the distance and bearing of the finishing point from the starting point.
| Let the starting point be O. The aircarft flies 500 km on bearing of 100°. It reaches point A Then 600 km on a bearing of 160°. Let the finishing point be X 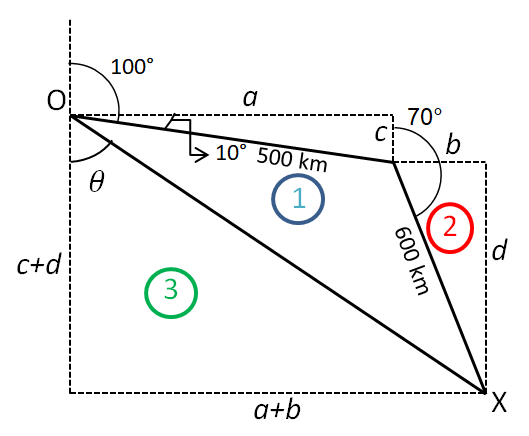 | Bearing is 100° i.e the total angle measured clockwise from North is 100°. The horizontal at O represents West. Therefore the angle between the line of travel of ship and West = 100°-90°=10° 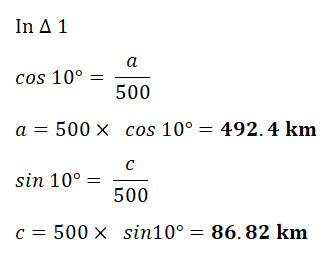 The bearing of aircraft is now 160°. Hence the angle it makes with the horizontal at point A is 160°-90°=70°  The total distance traveled along The total distance traveled along horizontal axis is a+b The total distance traveled along vertical axis is c+d  |
The Aircraft is at a distance of 953.8 km from the starting point.
The bearing of the finishing point is 180 - 47 = 133°
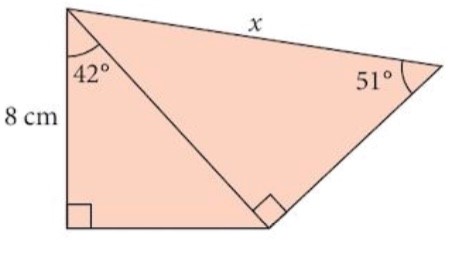
4. For the points P(2,5), Q(5,1) and R(0,-3), Calculate the angle PQR
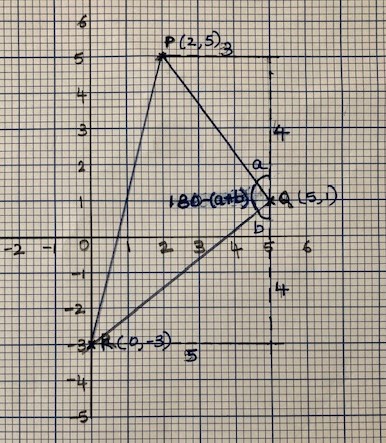 | 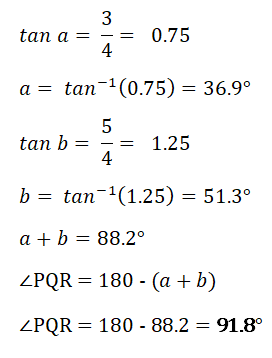 |
5. From the top of a tower 75 m, a man sees two goats, both due west of him.
If the angle of depression of the two goats are 10° and 17° respectively,
Calculate the distance between them.
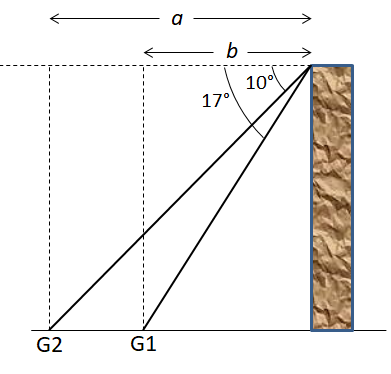 | Angle of depression of goat G1 = 17° Angle of depression of goat G2 = 10° 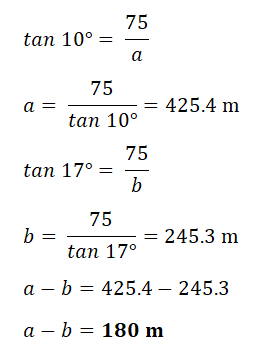 |
The distance between the goats is 180 m
Find the radius of the circle.
 | 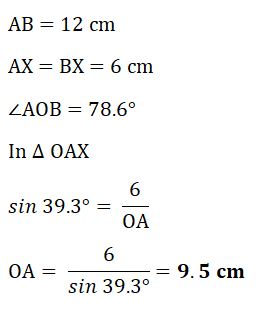 |
7. A rocket flies 10 km vertically, then 20 km at an angle of 15° to the vertical and finally 60 km at an angle of 26° to the vertical. Calculate the vertical height of the rocket at the end of the third stage.
 |  |

 | 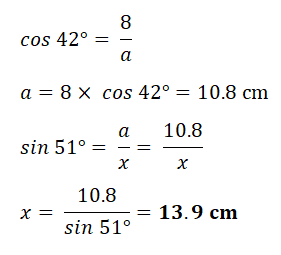 |
9. Diagram A shows a kitchen floor tiled with regular octagons and squares.
Diagram B shows and enlarged view of one octagon.

The smaller green squares have sides of length 12 cm.
Find the width of the octagons.
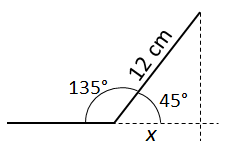 | Interior Angle of a regular Octagon = 135° Hence angle in triangle = 45° 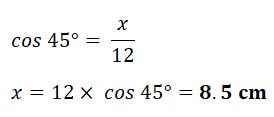 Width of Octagon = (8.5 X 2) + 12 Width of Octagon = (8.5 X 2) + 12= 29 cm |
10. A farm gate is 1.3 m high.
The diagonal crossbar has a width of 15 cm and makes an angle of 24° with the horizontal.
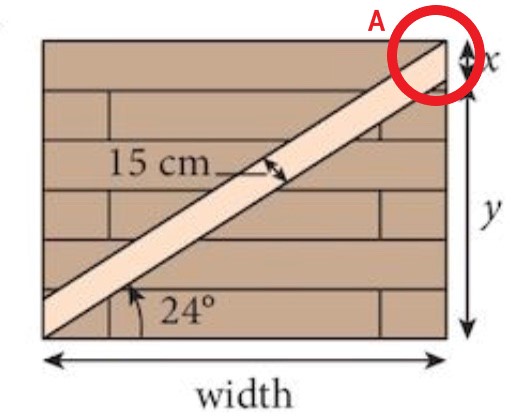
Find the length of x and y in the diagram.
Hence find the width of the gate.
POINT A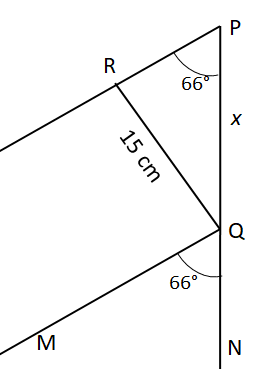 |   |
Width of gate = 255 cm

What is the height of the highest point of the stone above ground?
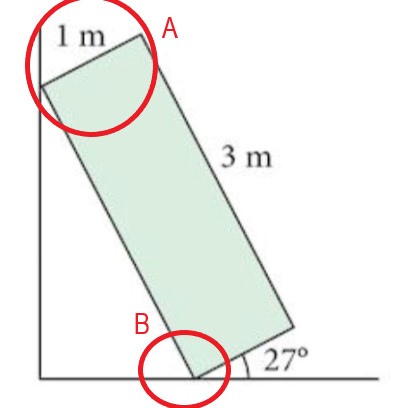 | Point B: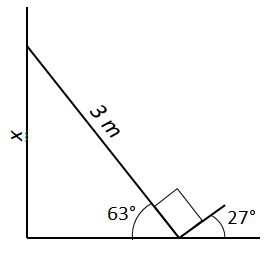 Point A: Point A: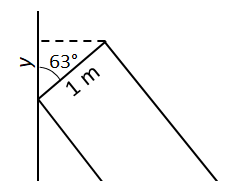 | 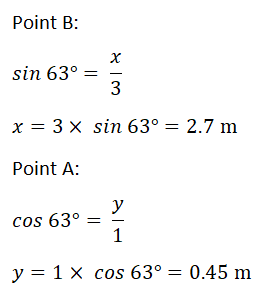 |
12. The diagram shows the cross section of a rectangular fish tank.

When AB is inclined at 40°, the water just comes up to A.
The tank is then lowered so that BC is horizontal.
What is now the depth of the water in the tank?
Figure 1: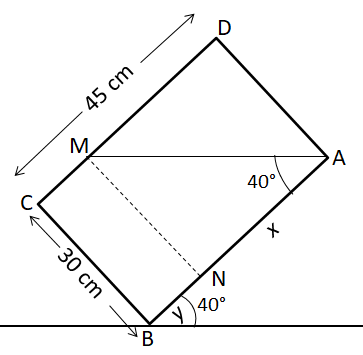 Figure 2: Figure 2: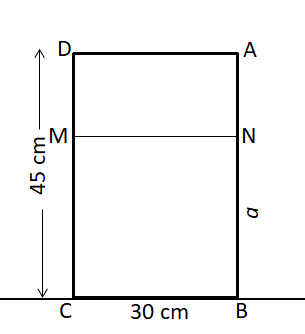 | The area in cross section of Figure 1 and area in cross section of figure 2 will be equal as the volume of water is the same. 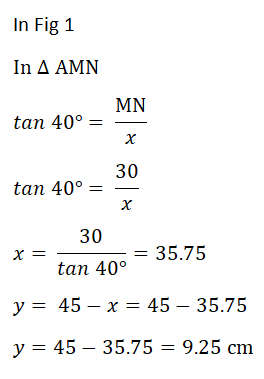  |