1. The diagram shows a prism ABCDEF.
The cross-section is a right angled triangle BCD.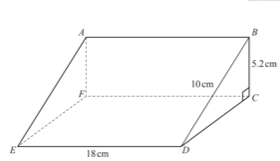
BD = 10 cm, BC = 5.2 cm and ED = 18 cm.
(i) a) Work out the volume of the Prism.
b) Calculate angle BEC
c) The point G lies on the line ED and GD = 7 cm. Work out angle BGE
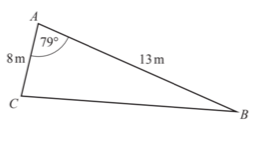
2. The diagram shows a triangle ABC.
The cross-section is a right angled triangle BCD.
BD = 10 cm, BC = 5.2 cm and ED = 18 cm.(i) a) Work out the volume of the Prism.
b) Calculate angle BEC
c) The point G lies on the line ED and GD = 7 cm. Work out angle BGE
(Cambridge Assessment International Education. 0580/42, October/November 2019, Q 4b)
| a) |  |
| b) |  |
| c) |    |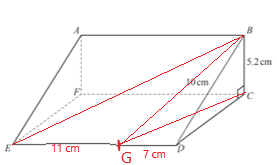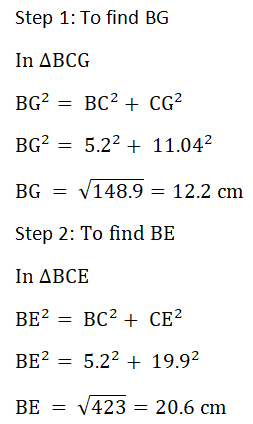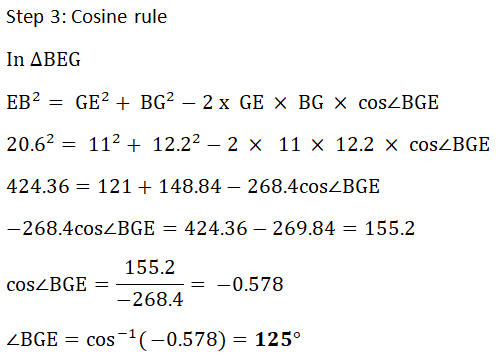
2. The diagram shows a triangle ABC.
(i) Use the cosine rule to calculate BC
(ii) Use the sine rule to calculate angle ACB
3. The bearing of P from B is 102°.
Find the bearing of B from P.
(Cambridge Assessment International Education. 0580/22, October/November 2019, Q 8)
4. The diagram shows two triangles ABD and BCD.
AD = 16.5 cm and BD = 12.4 cm. Angle ABD = 64°, angle BDC = 53° and angle DBC = 95°.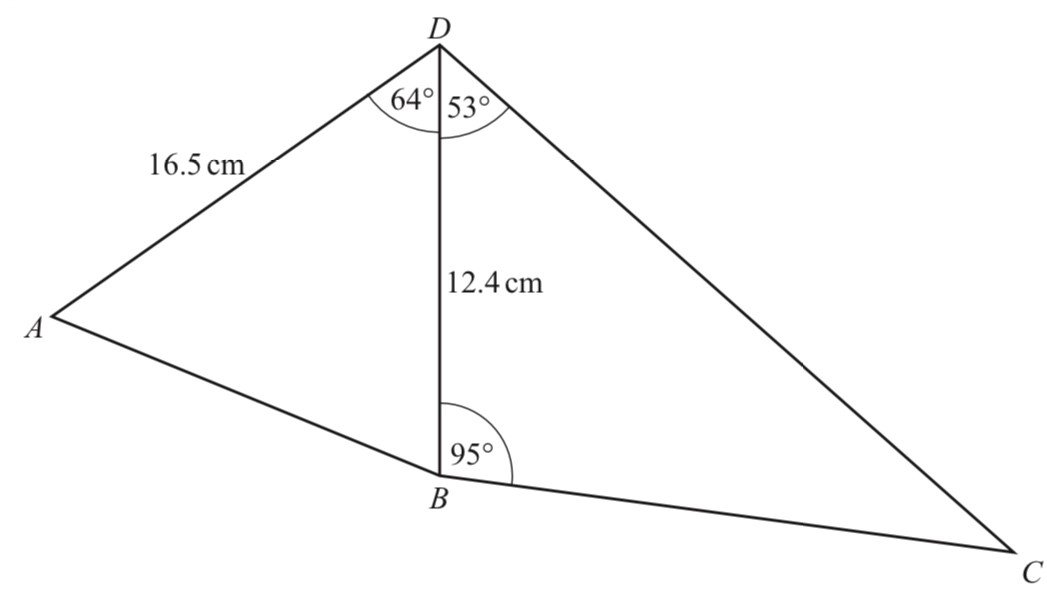
(i) Find AB
(ii) Find BC
5. ABCDEFGH is a cuboid.
AB = 18 cm, BC = 7 cm and CG = 12 cm.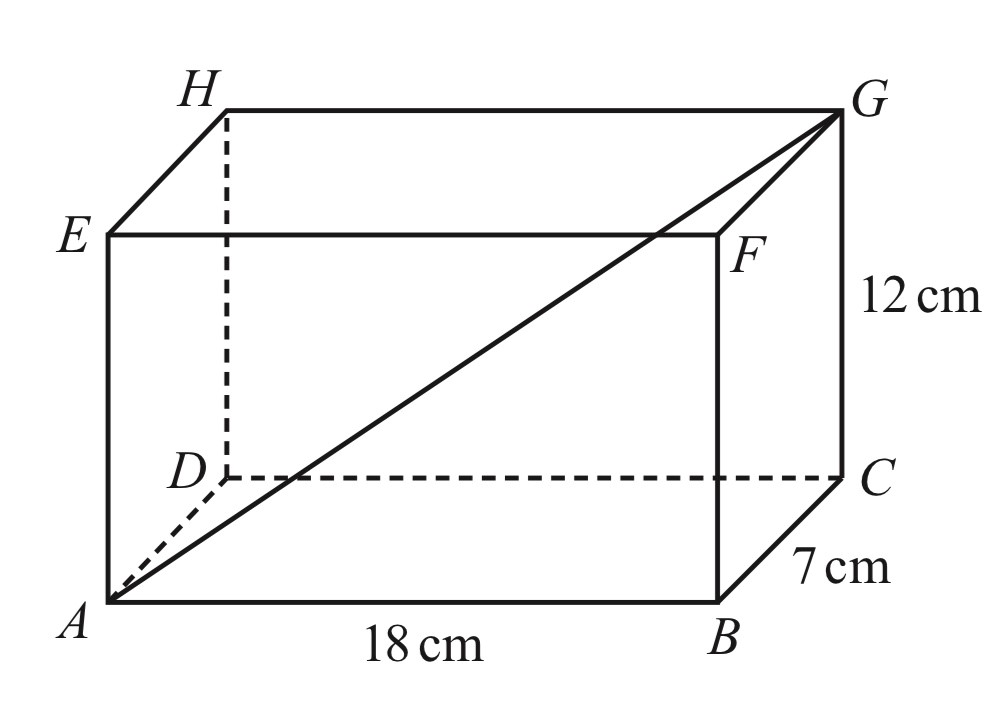
Calculate the angle that the diagonal AG makes with the base ABCD.
(Cambridge Assessment International Education. 0580/22, May/June 2019, Q 24)
6. Calculate:
(i) SR
(ii) RQ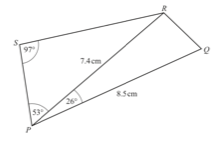
(Cambridge Assessment International Education. 0580/22, Feb/March 2019, Q 24)
7. The Diagram shows the Position of three cities Geneva(G), Budapest(B) and Hamburg(H).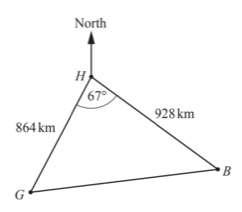
(i) Use the cosine rule to calculate the distance from Geneva to Budapest.
(ii) The bearing of Budapest from Hamburg is 133°.
(a) Find the bearing of Hamburg from Budapest
(b) Calculate the bearing of Budapest from Geneva.
(Cambridge Assessment International Education. 0580/42, Oct/Nov 2018, Q 8b, 8c)
8. The diagram shows a cuboid with dimensions with 5.5 cm, 8 cm and 16.2 cm.
9.The diagram shows a design made from a triangle ACO joined to a sector OCB.
AC = 8 cm, OB = OC = 7 cm and angle ACO = 78°.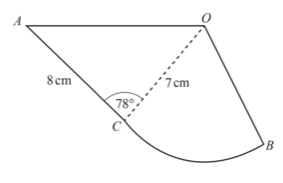
(a) Use the cosine rule to show that OA = 9.47 cm, correct to 2 decimal places.
(b) Calculate angle OAC.
(Cambridge Assessment International Education. 0580/42, May/June 2018, Q 5)
10. A and B are two towns on a map.
The bearing of A from B is 140°.
Work out the bearing of B from A.
11. The Diagram shows two ports L and P, and a buoy M.
The bearing of L from P is 201° and LP = 248 km.
The bearing of M from P is 127°. Angle PML = 42°.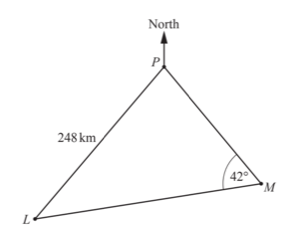
(a) Use the sine rule to calculate LM
(Cambridge Assessment International Education. 0580/42, Feb/Mar 2018, Q 8a)
12. The diagram shows a prism of length 4 cm.
The cross-section is a right angled triangle.
BC = 3 cm and CQ = 2cm.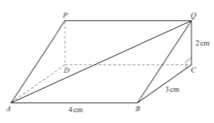
Calculate the angle between the line AQ and the base, ABCD, of the prism.
(Cambridge Assessment International Education. 0580/22, Oct/Nov 2017, Q 26)
13. The diagram shows a pyramid on a rectangular base ABCD.
AB and CD intersect at M and P is vertically above M.
AB = 8 cm, BC = 6 cm and PM = 9 cm.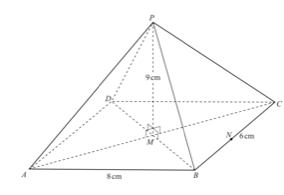
(a) N is the midpoint of BC
Calculate angle PNM
(b) Show that BM = 5 cm.
(c) Calculate the angle between the edge PB and the base ABCD
(d) A point X is on PC so that PX = 7.5 cm.
Calculate BX
(Cambridge Assessment International Education. 0580/22, May/June 2017, Q 8)
14. Calculate the value of x.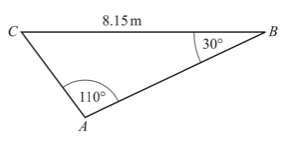
(Cambridge Assessment International Education. 0580/22, May/June 2017, Q 17)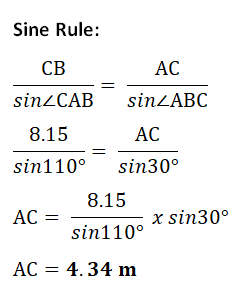 
Y is a point on the line XZ such that TY = 9.9 cm. angle XTY = 23° and angle TYZ = 72°.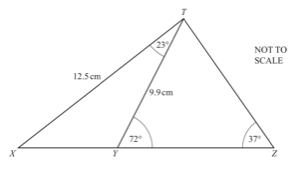
(i) Calculate XY
(ii) Calculate TZ
(Cambridge Assessment International Education. 0580/42, Feb/Mar 2017, Q 8a)
(ii) Use the sine rule to calculate angle ACB
(Cambridge Assessment International Education. 0580/42, October/November 2019, Q 6a)
| (i) |  |
| (ii) |  |
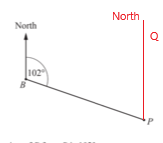
3. The bearing of P from B is 102°.
Find the bearing of B from P.
(Cambridge Assessment International Education. 0580/22, October/November 2019, Q 8)
  |  |
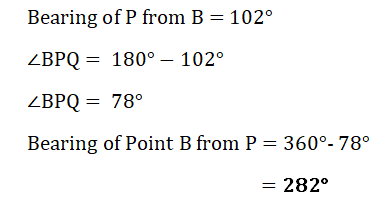4. The diagram shows two triangles ABD and BCD.
AD = 16.5 cm and BD = 12.4 cm. Angle ABD = 64°, angle BDC = 53° and angle DBC = 95°.
(i) Find AB(ii) Find BC
(Cambridge Assessment International Education. 0580/42, May/June 2019, Q 8a)
| (i) |  |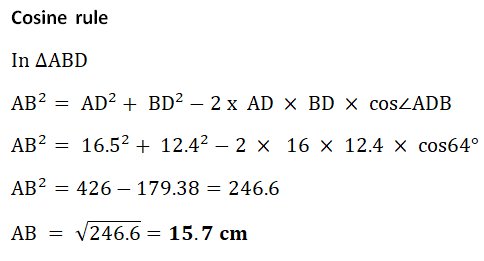
| (ii) |  |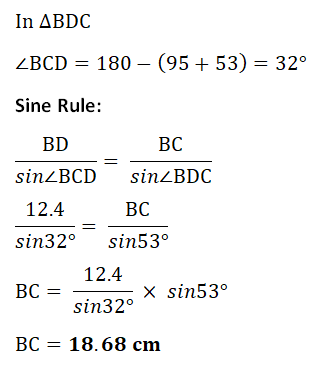
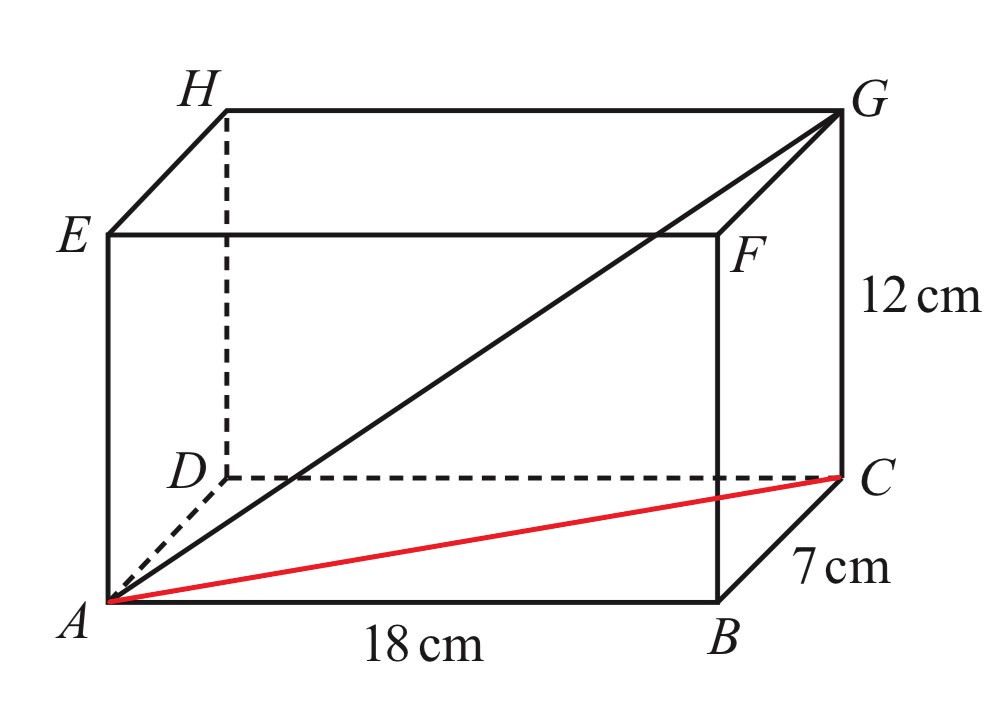
5. ABCDEFGH is a cuboid.
AB = 18 cm, BC = 7 cm and CG = 12 cm.
Calculate the angle that the diagonal AG makes with the base ABCD.(Cambridge Assessment International Education. 0580/22, May/June 2019, Q 24)
 |  |
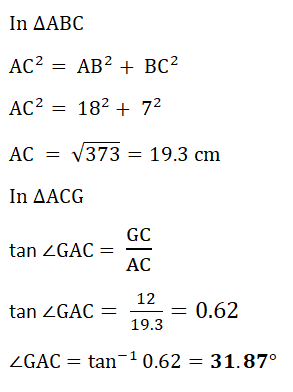6. Calculate:
(i) SR
(ii) RQ
(Cambridge Assessment International Education. 0580/22, Feb/March 2019, Q 24) | (i) |  |
| (ii) |  |
7. The Diagram shows the Position of three cities Geneva(G), Budapest(B) and Hamburg(H).
(i) Use the cosine rule to calculate the distance from Geneva to Budapest.(ii) The bearing of Budapest from Hamburg is 133°.
(a) Find the bearing of Hamburg from Budapest
(b) Calculate the bearing of Budapest from Geneva.
(Cambridge Assessment International Education. 0580/42, Oct/Nov 2018, Q 8b, 8c)
| (i) |  |
| (ii) (a) |  Bearing of Humburg from Budapest= 360° - 47° = 333° |
| (ii) (b) |  Bearing of Budapest from Geneva + 59.6 ° + 20° = 79.6° |
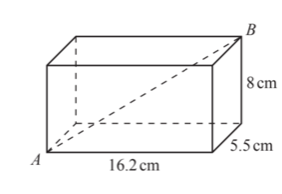
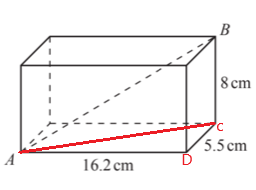
8. The diagram shows a cuboid with dimensions with 5.5 cm, 8 cm and 16.2 cm.
Calculate the angle between the line AB and the horizontal base of the cuboid.
(Cambridge Assessment International Education. 0580/22, Oct/Nov 2018, Q 22)
 |  |
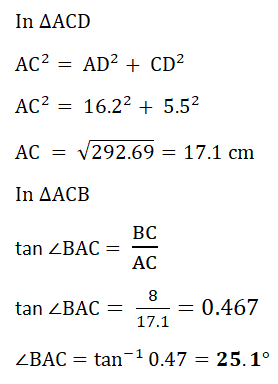9.The diagram shows a design made from a triangle ACO joined to a sector OCB.
AC = 8 cm, OB = OC = 7 cm and angle ACO = 78°.
(a) Use the cosine rule to show that OA = 9.47 cm, correct to 2 decimal places.(b) Calculate angle OAC.
(Cambridge Assessment International Education. 0580/42, May/June 2018, Q 5)
| (a) |  |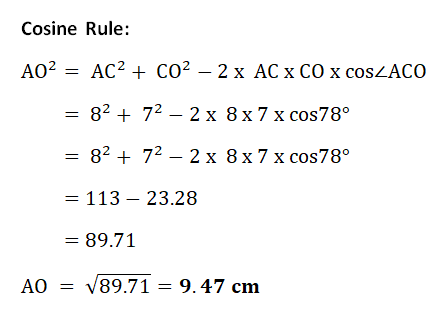
| (b) |  ∠OAC = 180 - ∠AOC - 78= 180 - 55.72 - 78 = 46.3° |
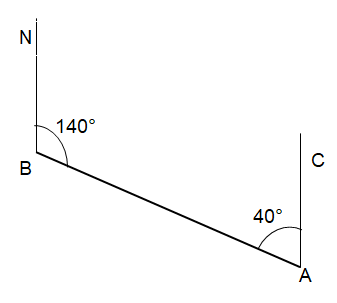
10. A and B are two towns on a map.
The bearing of A from B is 140°.
Work out the bearing of B from A.
(Cambridge Assessment International Education. 0580/22, May/June 2018, Q 7)
 |  |
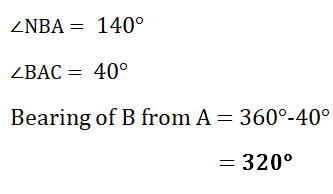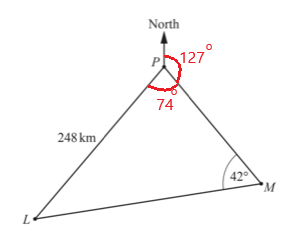
11. The Diagram shows two ports L and P, and a buoy M.
The bearing of L from P is 201° and LP = 248 km.
The bearing of M from P is 127°. Angle PML = 42°.
(a) Use the sine rule to calculate LM(Cambridge Assessment International Education. 0580/42, Feb/Mar 2018, Q 8a)
 |  |
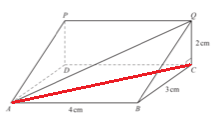
12. The diagram shows a prism of length 4 cm.
The cross-section is a right angled triangle.
BC = 3 cm and CQ = 2cm.
Calculate the angle between the line AQ and the base, ABCD, of the prism.(Cambridge Assessment International Education. 0580/22, Oct/Nov 2017, Q 26)
 |  |
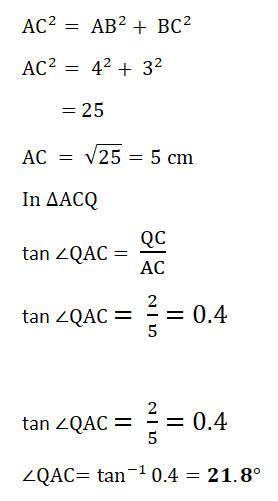13. The diagram shows a pyramid on a rectangular base ABCD.
AB and CD intersect at M and P is vertically above M.
AB = 8 cm, BC = 6 cm and PM = 9 cm.
(a) N is the midpoint of BC
Calculate angle PNM
(b) Show that BM = 5 cm.
(c) Calculate the angle between the edge PB and the base ABCD
(d) A point X is on PC so that PX = 7.5 cm.
Calculate BX
(Cambridge Assessment International Education. 0580/22, May/June 2017, Q 8)
| (a) |  |
| (b) |  |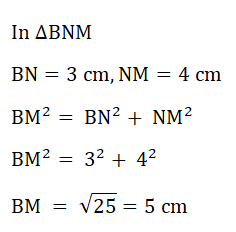
| (c) |  |
| (d) |    |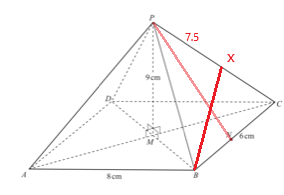
14. Calculate the value of x.
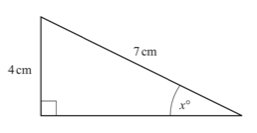
(Cambridge Assessment International Education. 0580/22, May/June 2017, Q 12)
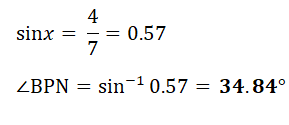
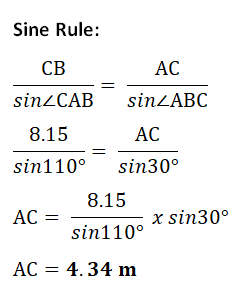
(Cambridge Assessment International Education. 0580/22, May/June 2017, Q 17) Y is a point on the line XZ such that TY = 9.9 cm. angle XTY = 23° and angle TYZ = 72°.
(i) Calculate XY(ii) Calculate TZ
(Cambridge Assessment International Education. 0580/42, Feb/Mar 2017, Q 8a)
| (i) |  |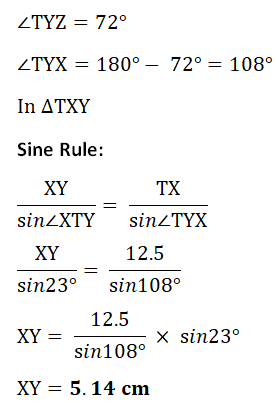
| (ii) |  |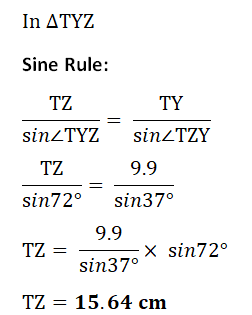
17. (a) The diagram shows a regular hexagon ABCDEF of side 10cm.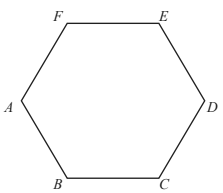
(i) Show that angle BAF = 120°.
(ii) The vertices of a rectangle PQRS touch the sides FA, AB, CD and DE.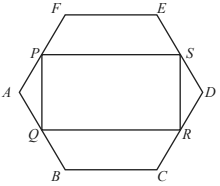
PS is parallel to FE and AP = x cm. Use trigonometry to find the length of PQ in terms of x.
(iii) PF = (10 – x) cm. Show that PS = (20 − x) cm.
(b) The diagram shows the vertices of a square KLMN touching the sides of the same hexagon ABCDEF,
with KN parallel to FE.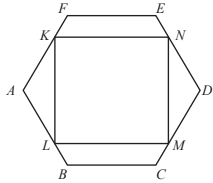
Use your results from part (a)(ii) and part (a)(iii) to find the length of a side of the square.
(Cambridge Assessment International Education. 0580/42, Feb/Mar 2017, Q 10)
18. The diagram shows a pyramid with a square base ABCD.
All the sloping edges of the pyramid are 20 cm long and AV = 17 cm.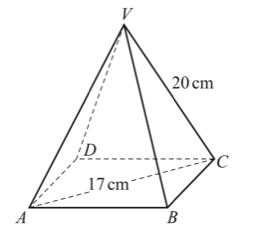
Calculate the height of the pyramid.
(Cambridge Assessment International Education. 0580/22, Feb/Mar 2017, Q 9)
(i) Show that angle BAF = 120°.(ii) The vertices of a rectangle PQRS touch the sides FA, AB, CD and DE.
PS is parallel to FE and AP = x cm. Use trigonometry to find the length of PQ in terms of x.(iii) PF = (10 – x) cm. Show that PS = (20 − x) cm.
(b) The diagram shows the vertices of a square KLMN touching the sides of the same hexagon ABCDEF,
with KN parallel to FE.
Use your results from part (a)(ii) and part (a)(iii) to find the length of a side of the square.(Cambridge Assessment International Education. 0580/42, Feb/Mar 2017, Q 10)
| (a)(i) |  |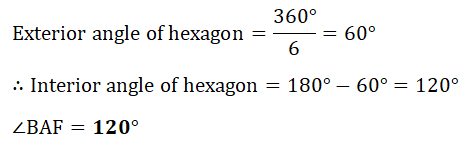
| (a)(ii) |  |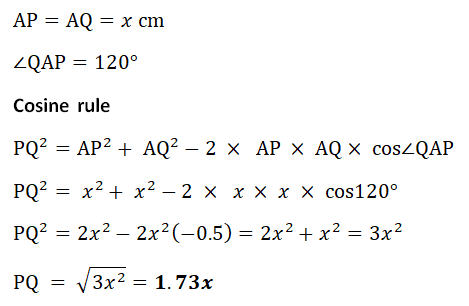
| (a)(iii) |   |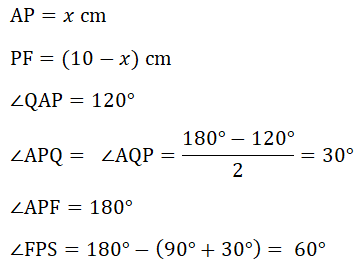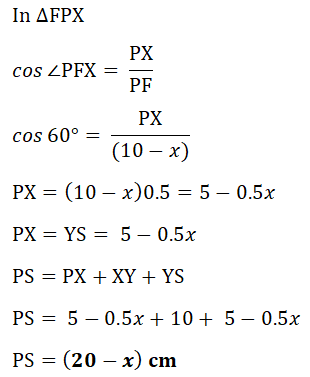
| (b) |  |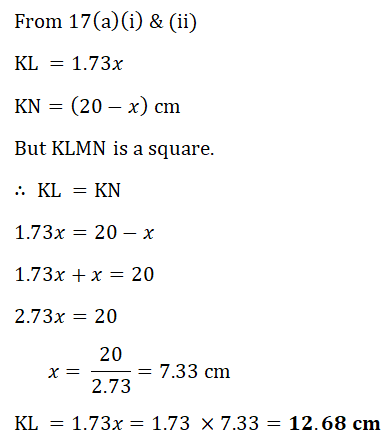
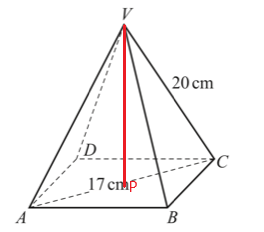
18. The diagram shows a pyramid with a square base ABCD.
All the sloping edges of the pyramid are 20 cm long and AV = 17 cm.
Calculate the height of the pyramid.(Cambridge Assessment International Education. 0580/22, Feb/Mar 2017, Q 9)
 |  |